ABC016 D - 一刀両断

他のブログを見て「なんで交差判定"2回"してるの？？」と思った人用の記事。

問題

abc016.contest.atcoder.jp

多角形と、線分が与えられる。線分により、多角形はいくつの領域に分断されるか。

解法

公式の解答を見ると、(求める数) = (線分と交差する辺の数) / 2 + 1 であり、線分と辺の交差判定には符号つき面積を用いればよいことが分かる。しかしここで注意すべきは、あくまで「線分と線分との交差判定」であるということ。

直線と線分の交差判定なら簡単だ。下において点Pと点Qが直線ABに関して反対側にあることと、三角形ABPと三角形ABQの面積が異符号が同値である。

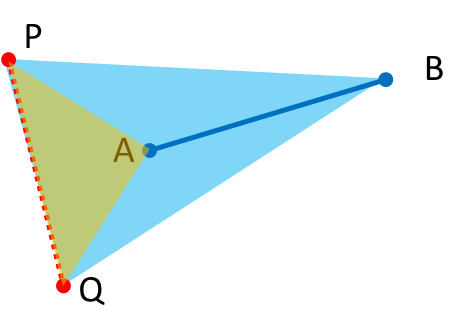
しかしこれだけだと、図2のような場合にも交差していると判定してしまう。

そこで線分ABと線分PQが交差しているかどうかを判定するには、下図のように、直線PQに関して点A, Bが反対側にあるかどうかも判定しなければならない。

まとめる。

線分ABと線分PQが交差していることは、つぎの1かつ2を満たすことと同値である。 1. 直線ABに関して点P, Qが反対側にある 2. 直線PQに関して点A, Bが反対側にある

• 解答例: C++

double Ax, Ay, Bx, By;
int N;
double X[MAX_N], Y[MAX_N];

void input() {
    cin >> Ax >> Ay >> Bx >> By;
    cin >> N;
    REP(i, N) {
        cin >> X[i] >> Y[i];
    }
}

double area(double x1, double y1, double x2, double y2, double x3, double y3) {
    return (x1 - x3) * (y2 - y3) - (x2 - x3) * (y1 - y3);
}

bool check(int i) {
    // チョップから見て辺の両端点が同じ側なら交差しない
    if (area(X[i], Y[i], Ax, Ay, Bx, By) * area(X[(i+1) % N], Y[(i+1) % N], Ax, Ay, Bx, By) >= 0)
        return false;

    // 辺から見てチョップの両端点が同じ側なら交差しない
    if (area(Ax, Ay, X[i], Y[i], X[(i+1) % N], Y[(i+1) % N]) * area(Bx, By, X[i], Y[i], X[(i+1) % N], Y[(i+1) % N]) >= 0)
        return false;

    // どちらから見ても逆側だったら線分は交差している
    return true;

}

void solve() {
    int cnt = 0;
    REP(i, N) {
        cnt += check(i);
    }
    cout << cnt / 2 + 1 << endl;
}


int main() {
    input();
    solve();
    return 0;
}

「線分の交差判定」を理解して1ヶ月ごしのAC。